Including relevant XKCD as demanded by internet law: https://xkcd.com/10/

Oooh, a rare two-digit.
Eating the onion is sure popular today!
they didn’t?
If pi is truly infinite, then it contains all the works of Shakespeare, every version of Windows, and this comment I’m typing right now.
That’s not how it’s works. Being “infinite” is not enough, the number 1.110100100010000… is “infinite”, without repeating patterns and dosen’t have other digits that 1 or 0.
to be fair, though, 1 and 0 are just binary representations of values, same as decimal and hexadecimal. within your example, we’d absolutely find the entire works of shakespeare encoded in ascii, unicode, and lcd pixel format with each letter arranged in 3x5 grids.
Doesn’t, the binary pattern 10101010 dosen’t exists on that number, for example.
You can encode base 2 as base 10, I don’t think anyone is saying it exists in binary form.
Well it’s infinite so it has to I guess
Does this count:
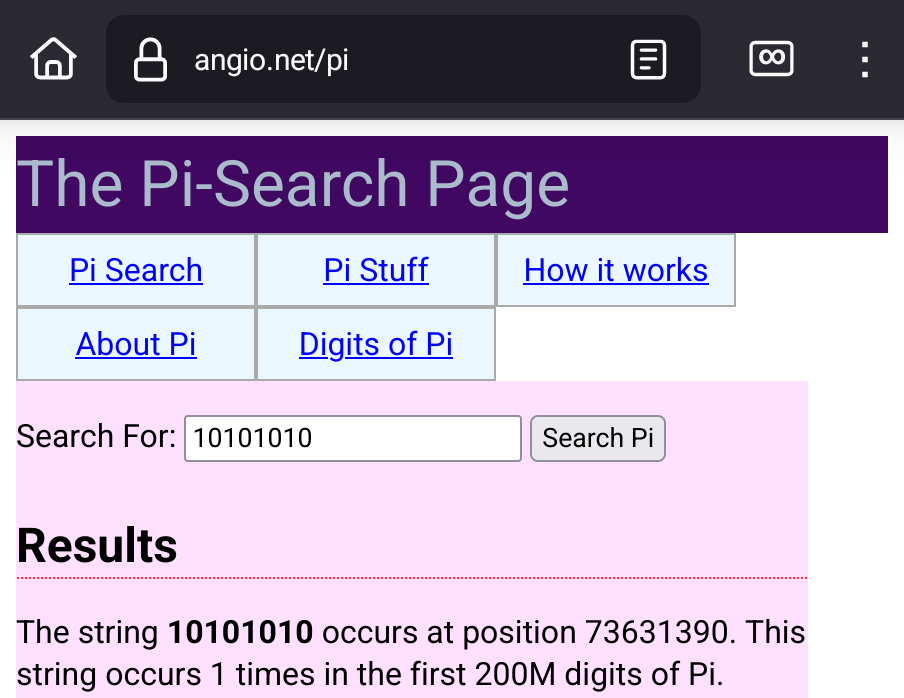
No, because you can’t mathematically guarantee that pi contains long strings of predetermined patterns.
The 1.101001000100001… example by the other user was just that - an example. Their number is infinite, but never contains a 2. Pi is also infinite, but does it contain the number e to 100 digits of precision? Maybe. Maybe not. The point is, we don’t know and we can’t prove it either way (except finding it by accident).
Actually, there’d only be single pixels past digit 225 in the last example, if I understand you correctly.
If we can choose encoding, we can “cheat” by effectively embedding whatever we want to find in the encoding. The existence of every substring in a one of a set of ordinary encodings might not even be a weaker property than a fixed encoding, though, because infinities can be like that.
If it’s infinite without repeating patterns then it just contain all patterns, no? Eh i guess that’s not how that works, is it? Half of all patterns is still infinity.
No. 1011001110001111… (One 1, one 0, two 1s, two zeros…) Doesn’t contain repeating patterns. It also doesn’t contain any patterns with ‘2’ in it.
But pi is believed to be normal. https://en.m.wikipedia.org/wiki/Normal_number
So it should contain all finite patterns an infinite number of times.
However, as the name implies, this is nothing special about pi. Almost all numbers have this property. If anything, it’s the integers that we should be finding weird, like you mean to tell me that every single digit after the decimal point is a zero? No matter how far you go, just zeroes forever?
Yeah, but your number doesn’t fit pi. It may not have a pattern, but it’s predictable and deterministic.
Pi is predictable and deterministic.
Computer programs exist that can tell you what the next digit is. That means it’s deterministic, and running the program will give you a prediction for each digit (within the memory constraints of your computer).
The fact that it’s deterministic is exactly why pi is interesting. If it was random it would typically be much easier to prove properties about it’s digits.
There’s no way to predict what the next unsolved pi digit will be just by looking at what came before it. It’s neither predictable nor deterministic. The very existence of calculations to get the next digit supports that.
Note: I’m not saying Pi is random. Again, the calculations support the general non-randomness of it. It is possible to be unpredictable, undeterministic, and completely logical.
Note Note: I don’t know everything. For all I know, we’re in a simulation and we’ll eventually hit the floating point limit of pi and underflow the universe. I just wanted to point out that your example doesn’t quite fit with pi.
π isn’t deterministic? How do you figure that? If two people calculate π they get different answers?
What π is, is fully determined by it’s definition and the geometry of a circle.
Also, unpredictable? Difficult to predict, sure. Unpredictable by simple methods, sure. But fully impossible to predict at all?
deleted by creator
Not, the example I gave have infinite decimals who doesn’t repeat and don’t contain any patterns.
What people think about when said that pi contain all patters, is in normal numbers. Pi is believed to be normal, but haven’t been proven yet.
An easy example of a number who contains “all patterns” is 0.12345678910111213…
Yes that’s why they specified pi.
Still not enough, or at least pi is not known to have this property. You need the number to be “normal” (or a slightly weaker property) which turns out to be hard to prove about most numbers.
Wikipedia for normal numbers, and for disjunctive sequences, which is the slightly weaker property mentioned.
> natural numbers
> rational numbers
> real numbers
> regular numbers
> normal numbers
> simply normal numbers
> absolutely normal numbersHave mathematicians considered talking about what numbers they find okay, rather than everyone just picking their favorite and saying that one’s the ordinary one?
I mean, unironically yes. It seems the most popular stance is that all math regardless of how weird is Platonically real, although that causes some real bad problems when put down rigorously. Personally I’m more of an Aristotelian.
In the case of things like rational or real numbers, they have a counterpart that’s weirder (irrational and imaginary numbers). For the rest I’m not sure, but it’s pretty common to just pick an adjective for a new concept. There’s even situations where the same term gets used more than once in different subfields, and then they collide so you have to add another one to clarify.
For example, one open interval in the context of a small set of open intervals isn’t closed analytically under limits, or algebraically closed, but is topologically closed (and also topologically open, as the name suggests).
“Nearly all real numbers are normal (basically no real numbers are not normal), but we’re only aware of a few. This one literally non-computable one for sure. Maybe sqrt(2).”
Gotta love it.
We’re so used to dealing with real numbers it’s easy to forget they’re terrible. These puppies are a particularly egregious example I like to point to - functions that preserve addition but literally black out the entire x-y plane when plotted. On rational numbers all additive functions are automatically linear, of the form mx+n. There’s no nice in-between on the reals, either; it’s the “curve” from hell or a line.
Hot take, but I really hope physics will turn out to work without them.
Simply containing each number sequence is a significantly weaker property than having them all occur at the right frequency. Still, while nobody has proven it, it’s generally expected to be true.
In some encoding scheme, those digits can represent something other than binary digits. If we consider your string of digits to truly be infinite, some substring somewhere will be meaningful.
One of the many things I loved about Sagan’s Contact is that, at the end, they found a pattern in pi when put into base 13. He didn’t really go into it as it was the end of the book, but I really wish he’d survived to write a sequel.
This person doesn’t understand infinity. Don’t feel bad, no one really does, it sort of breaks our brains.
shaves the sphere down with a sculptor’s knife
There. 3.1416. Not perfectly round but it’ll bake in the oven just fine.
I ate The Onion
Tbf I’ve heard crazier things which have ended up being true in the past week alone…
Microsoft sues the Library of Babel
“I may be a staunch atheist,” said Richard Stallman, creator of the GNU + Linux operating system and self-proclaimed architect of the modern world, “but any decent analysis in comparative religion would conclude that the universe is a copyleft creation, thereby pi should automatically fall under the terms of the GNUv3 license.”
Lol, he would actually say that
Is there an algorithm or number such that we could basically pirate data from it by saying “start digit 9,031,643,679 with length 5,345,109 is an MP4 of Shrek”? Something that we could calculate in a day or less?
The short answer is no, and even if we could, the digit index you’d start at would have a larger binary representation than the actual data you were trying to encode.
deleted by creator
An example I found: the string of digits 0123456789 occurs at position 17387594880. In this case, it took 11 digits to describe where to find a 10-digit number.
So I think such an algorithm would technically work, but your “start digit” would be so large it would use more data than just sending the raw file data. Not to mention the impossible amount of computing power needed.
What if instead we utilized an algorithm, some code, that would ultimately generate the file? I could imagine a program that generates a number which ultimately is more dense than the program. For example, if we just-so-happened to need a million digits of Pi the program would be shorter than the number. Is there a way to tailor an algorithm to collapse down to any number? As an example, what if we needed a million digits of Pi but the last 10 digits need to be all 9s?
Similarly: if you write a program to randomly run through all the combinations of pixels on a decently large screen (say, 1080p) you will eventually see every important question and answer that can be expressed on a screen.
Could we already do this by leveraging the Library of Babel?
Genuinely asking, I’m not really sure.
you can bookmark(?) pages
Conceptually this is basically just standard encryption: some math that spits out gibberish unless you have the info to make that gibberish become something useful.
I think if you can ridiculously compress the size down then maybe lol.
Do you happen to know of any good algorithms or numbers? Pi gets harder to calculate with each digit, so it’s not a great candidate.
This just in: Measurements are now limited to ~3M decimals.
Science is ruined!
Welp, time for quectoquectoquectoquectoquectometers.
Actually, a plank length seems to be 10 microquectometers, so my first guess might only be necessary for interpretation of the world, and not physical accuracy.
And I thought that was a measuring unit for ducks
There’s no way the copyright office is actually going to approve this right?
I think this is satire. Poe’s law is stronger than ever
deleted by creator
According to Dr. Calibri, there’s a 99.9999% chance they will approve it :)
Omg. Calibri… Didnt catch that the first time around lol














