We call two numbers x,y coprime if their greatest common divisor is 1.
Examples
- 9 and 8 are coprime
- 3 and 7 are coprime.
gcd(3, 7) = 1 - 11 and 99 are not coprime, since
gcd(99,11) = 11 != 1
Lower Diagonal y>x
A pixel x,y is marked black, if x and y are coprime.
Upper Diagonal x>y
A pixel x,y is marked black, if 2x+1 and 2y+1 are coprime
The different behavior for the upper/lower diagonal was chosen, since gcd is commotative, and the result would have been a boring mirror image.
generated with the following c-code:
#include "intmaths.h"
#include <stdio.h>
#include <assert.h>
int main(void){
// tests to check if gcd works
assert(3 == gcd(3*5, 3*7));
assert(11 == gcd(11*5, 11*7));
assert(1 == is_prime(3));
int t1 = gcd(11*3*3, 3*7);
assert(t1 == 3);
int t2 = gcd(11*4, 4*7);
assert(t2 == 4);
int W = 300;
int H = 300;
int START = 2;
printf("P1\n%d %d\n", W-START, H-START);
for(int y=START; y<H; y++){
for(int x=START; x<W; x++){
int r2 = 0;
if(x > y){
// upper diagonal
int xmod = 2*x+1;
int ymod = 2*y+1;
int gc = gcd(xmod, ymod);
if(gc == 1){
r2 = 1;
}// pixel is marked black, if xmod and ymod are coprime, and we are in upper diagonal
}else{
int gc = gcd(x, y);
if(gc == 1){
r2 = 1;
}
}
// int r2 = r % 2;
printf("%d", r2);
}
printf("\n");
}
return 0;
}
gcd was calcualted using euclids algorithm.
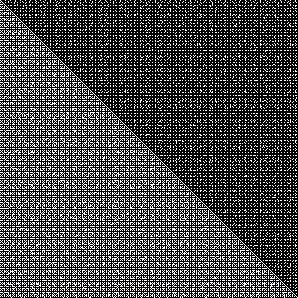
(͡•_ ͡• )
This doesn’t seem to scan as a QR code (yet)…
Have you tried running it through Conway’s Game Of Life?
I will try to randomize further using stopping time of the 3x+1 problem
But running cellular automata on the generated data also sounds fun!
I was thinking the image looks quite noisy, the image detail randomness can only truly be appreciated if “zoomed in”.
- should I use fourier transformations on this to make this happen
- are there other transformations that achieved this “turning scale inside out” effect … correlation functions?


