Today we want to generate this star like shape using sums of trigeometric functions sin and cos:

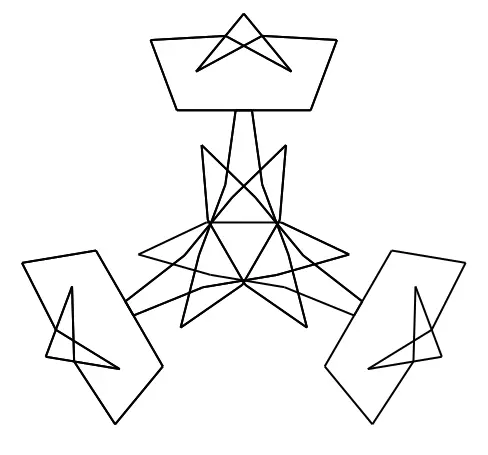
Function:

f(x) = x/57 + x**3/19 

where x**3 is x^3 = x*x*x written in python

To calculate the x and y coordinate of the nth. step:

sx(n) = sum((75*cos(2*pi*f(i)) for i in range(n)))
sy(n) = sum((75*sin(2*pi*f(i)) for i in range(n)))

To render this with pythons turtle library, the following code can be used.

from math import cos, sin, pi, tan
def f(x):
    form = x/57 + x**3/19
    return form

def seq(fu):
    r = 75 # "zoom" level, kinda arbitrary choice so you can see it well
    s = [0, 0]
    for i in range(10000):
        s[0] += r*cos(2*pi*fu(i))
        s[1] += r*sin(2*pi*fu(i))
        yield s

import turtle
from time import sleep
for i in seq(f):
    turtle.setpos(i[0], i[1])
sleep(20)

This exponential sum with function f seems to have a limited convergence-radius / the sum stays in a bounded circle for longer than 10000 steps in my experiments. Can you proof this?

Further reading:

• https://en.wikipedia.org/wiki/Exponential_sum
• https://anvaka.github.io/e-sum/?code=x%2F57+%2B+x*x*x%2F19&bufferSize=12000&totalSteps=12000&spi=500