- cross-posted to:
- generative@lemmy.ml
- cross-posted to:
- generative@lemmy.ml
Today we want to generate this star like shape using sums of trigeometric functions sin and cos:
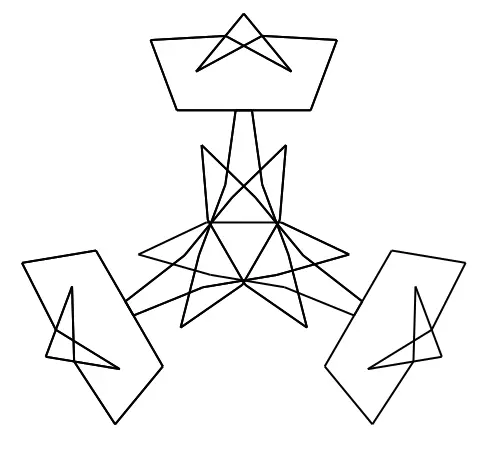
Function:
f(x) = x/57 + x**3/19
where x**3 is x^3 = x*x*x written in python
To calculate the x and y coordinate of the nth. step:
sx(n) = sum((75*cos(2*pi*f(i)) for i in range(n)))
sy(n) = sum((75*sin(2*pi*f(i)) for i in range(n)))
To render this with pythons turtle library, the following code can be used.
from math import cos, sin, pi, tan
def f(x):
form = x/57 + x**3/19
return form
def seq(fu):
r = 75 # "zoom" level, kinda arbitrary choice so you can see it well
s = [0, 0]
for i in range(10000):
s[0] += r*cos(2*pi*fu(i))
s[1] += r*sin(2*pi*fu(i))
yield s
import turtle
from time import sleep
for i in seq(f):
turtle.setpos(i[0], i[1])
sleep(20)
This exponential sum with function f seems to have a limited convergence-radius / the sum stays in a bounded circle for longer than 10000 steps in my experiments. Can you proof this?
Further reading:
You must log in or register to comment.
I call it pointer 3x ultrastar it shall be my greatest discovery, if someone else finds an earlier reference to this, please share haha.

